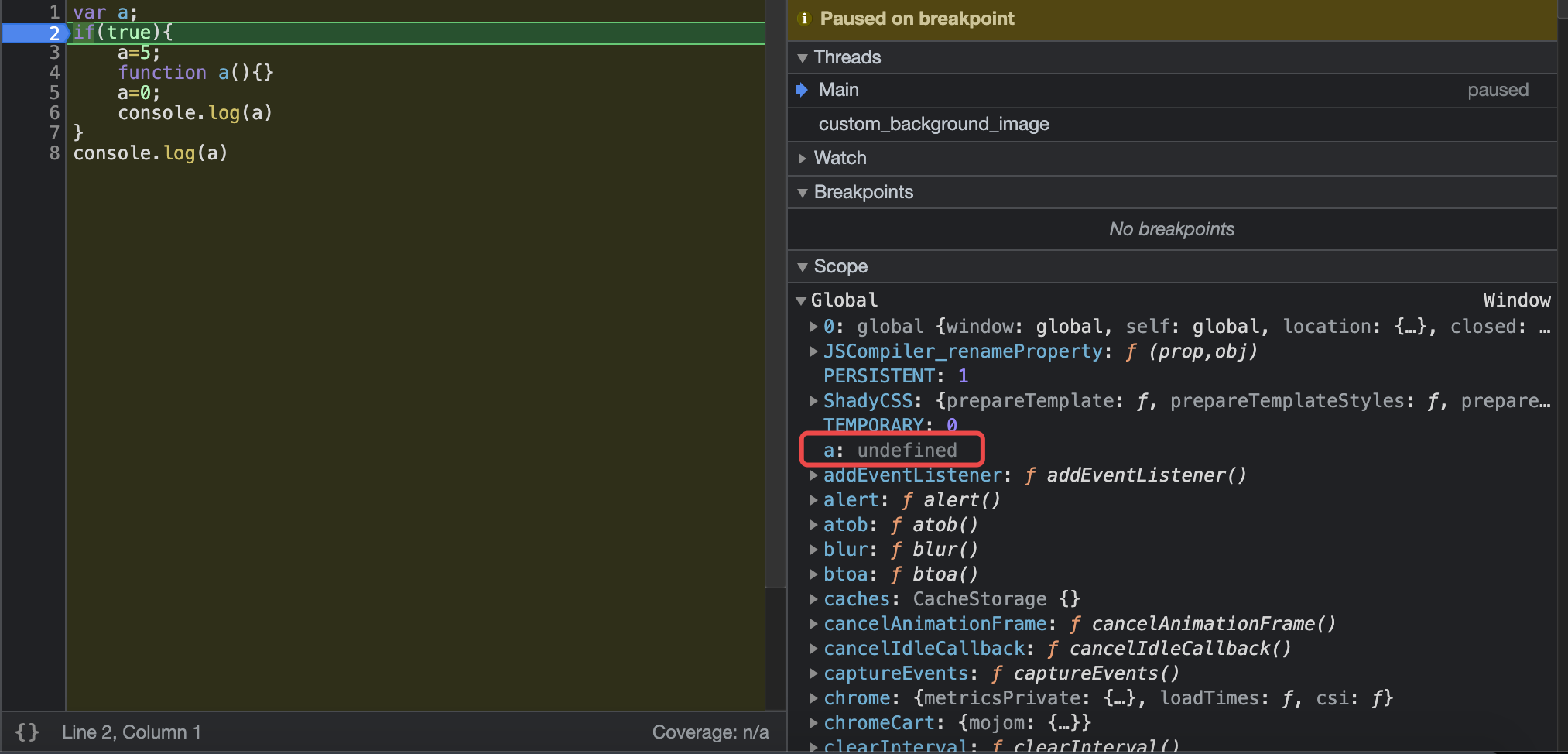
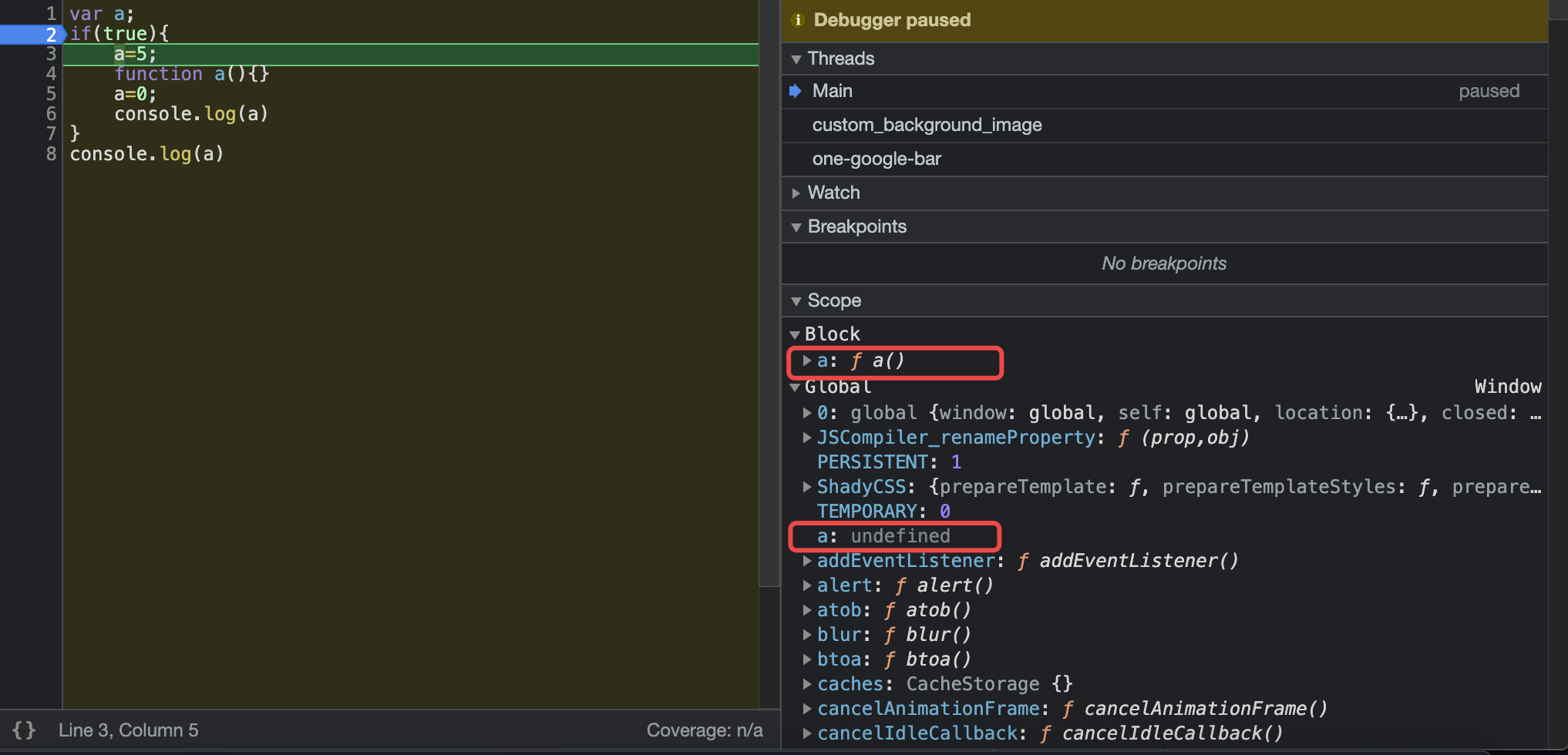
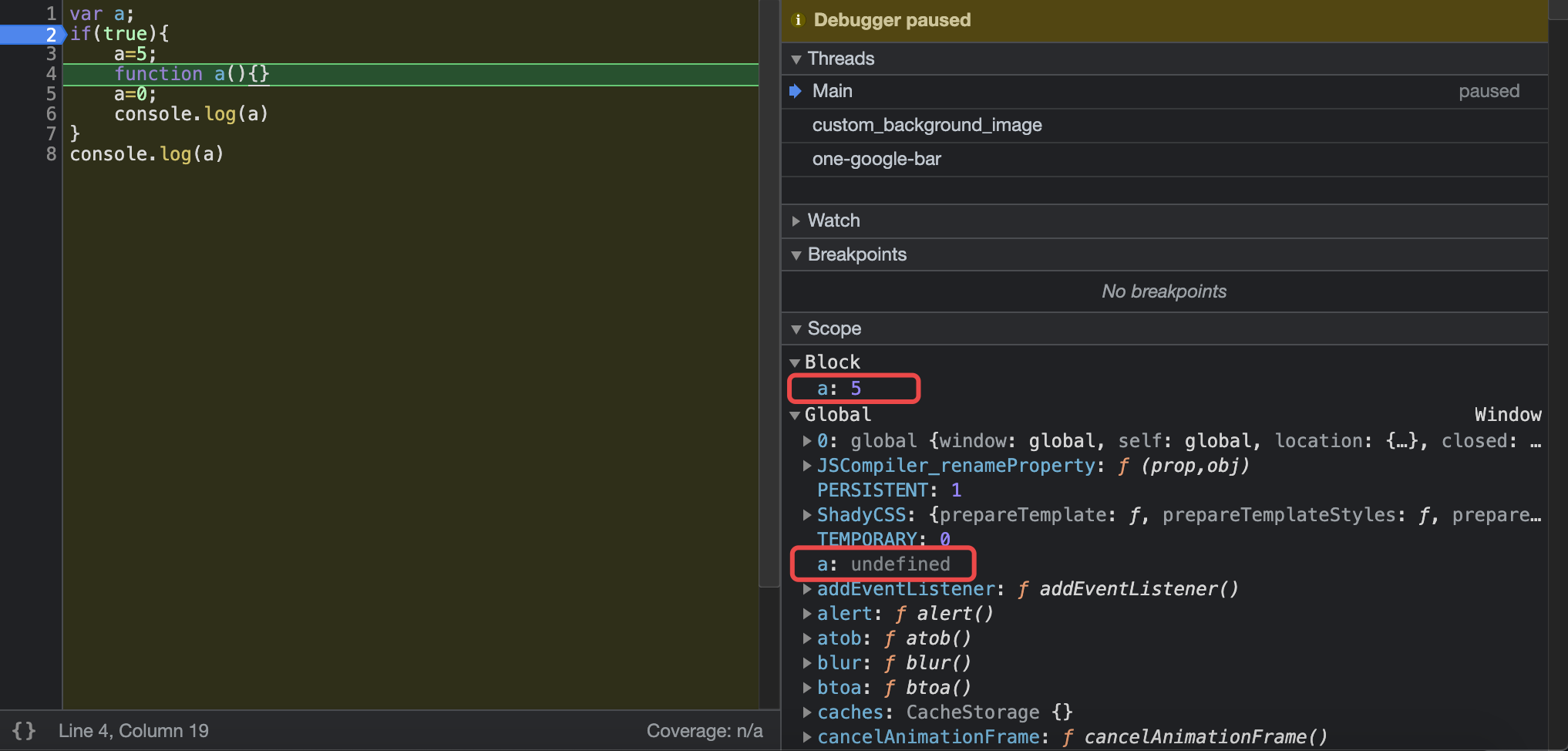
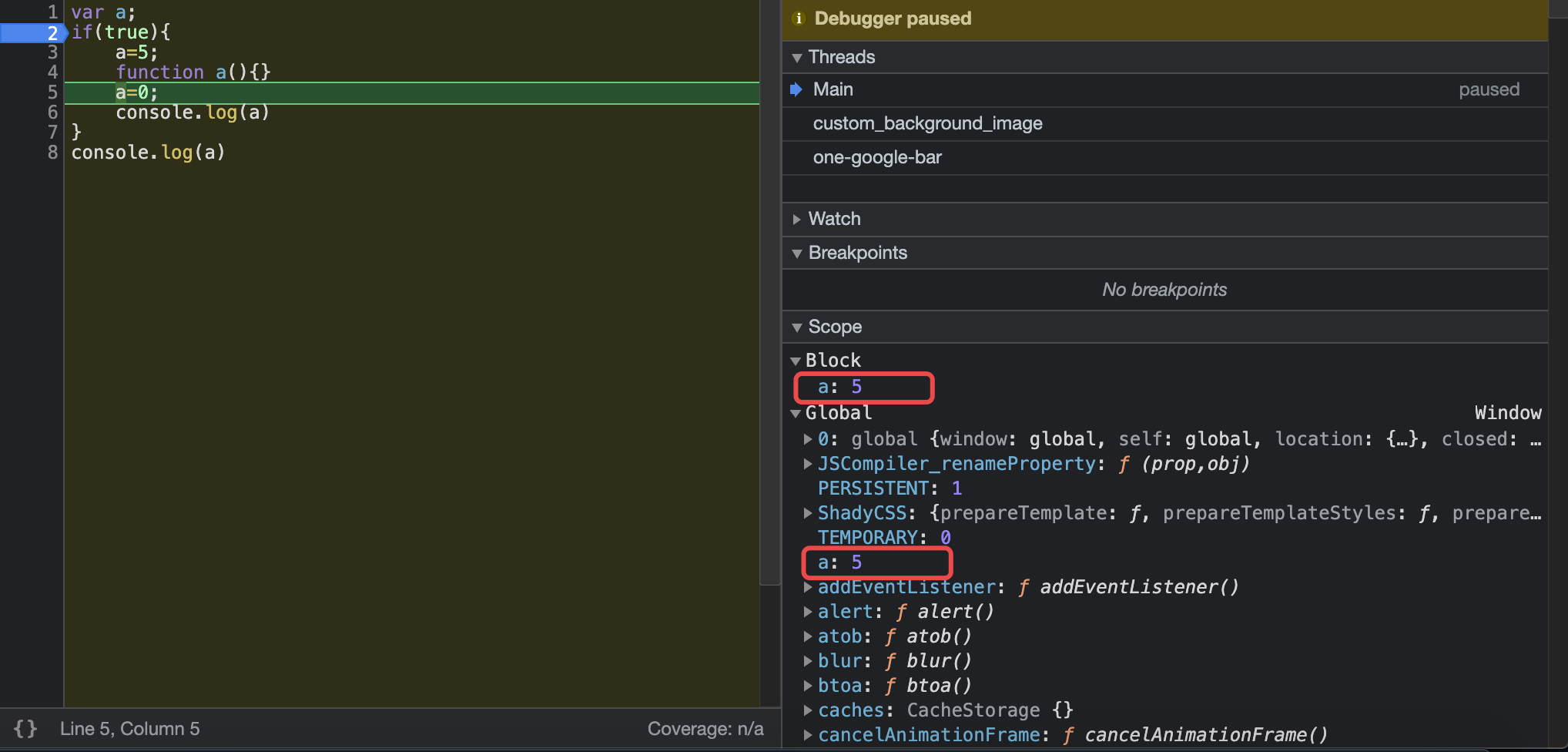
浏览器进程和线程
众所周知,浏览器每次在打开一个新页面的时候会创建一个独立于其他页面的Render进程 (渲染进程) ,而在这个渲染进程中包含了页面的渲染、JS的执行、事件的循环(Event Loop)等任务
重点概念:浏览器的渲染进程是多线程的
下面列举一下渲染进程的常驻线程:
- GUI渲染线程
- JS引擎线程
- 事件触发线程
- 定时触发器线程
- 异步http请求线程
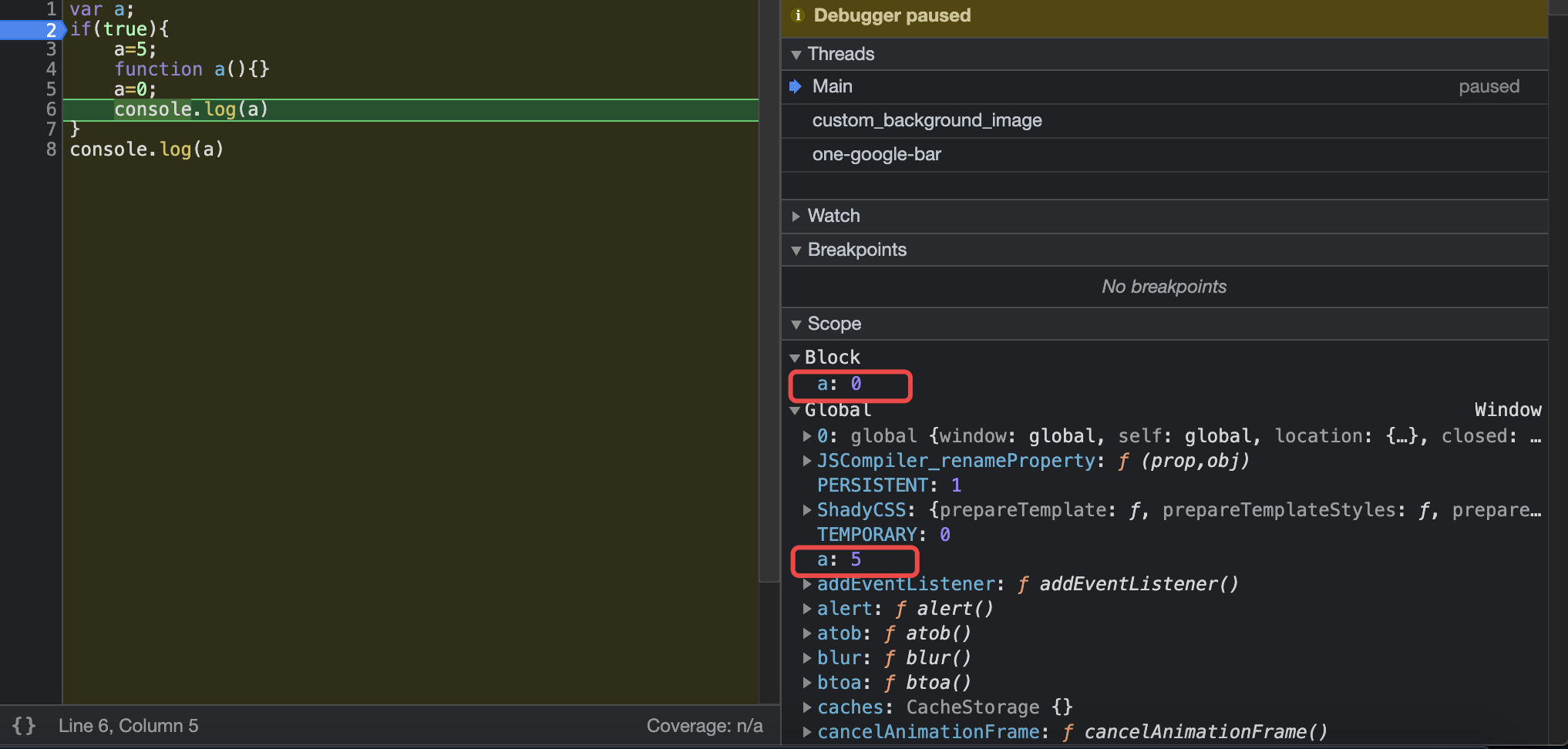
我们需要注意:GUI渲染线程和JS引擎线程是互斥的(由于JS能操作DOM,浏览器防止渲染出现不可预料的后果,将这两个线程设置为互斥),这也就意味着如果出现密集型的JS操作,将会堵塞GUI渲染进程,从而导致网页卡顿
Tips:JS引擎是单线程的,尽管多线程功能强大,但是线程同步比较复杂,并且危险,稍有不慎就会崩溃死锁。单线程的好处就是不必考虑线程同步这样的复杂问题,简单而安全。如果需要真正的多线程JS可以使用Web Worker,它可以使密集的运算跑在另一个线程中,但为了安全起见,你不能直接在 worker 线程中操纵 DOM 元素;或使用window 对象中的某些方法和属性。(详情请看MDN中关于Web Worker的说明)
旧的React Reconciler
在React15及以前,React通过递归的方式创建虚拟dom,而这个过程是不可中断的,因此如果组件树的层级很深就会出现递归时间过长的情况。在这种情况下,JS线程中长时间的递归运算会阻塞GUI渲染线程,从而造成网页卡顿。
React团队为了解决这个问题,以及为了React未来的发展,花了很长的时间重构Reconciler。现在我们使用的react Reconciler是基于Fiber架构的,从不可中断的递归方式变成了可中断的异步方式
如果用图片来描述上述变化: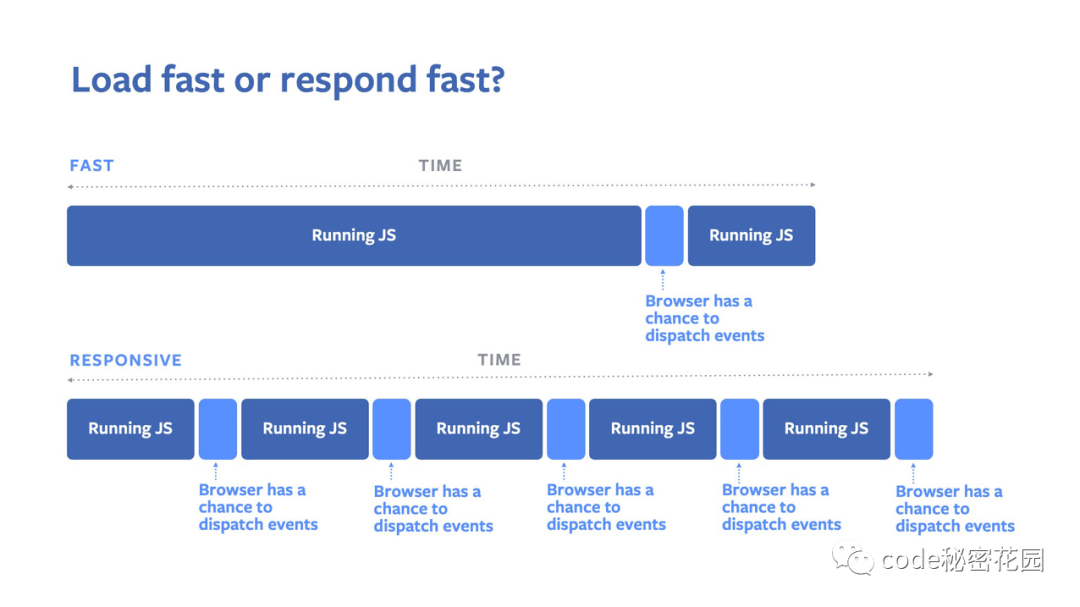
可以看到,原来的一整块JS密集运算(对应旧版Reconciler虚拟DOM的更新)成功被分割成了很多个子部分,这意味着浏览器的渲染进程每隔一段时间就能从JS线程中拿回控制权,完成其他必不可少的任务(例如GUI渲染线程、事件触发线程等),这样在高密度计算中渲染进程仍然有足够的机会去绘制页面,页面的卡顿问题迎刃而解。
新的React Reconciler
旧版的Reconciler工作方式采用递归调用,数据保存在递归调用栈中,因此也被称为Stack Reconciler;而新版Reconciler基于Fiber数据结构,因此被称为Fiber Reconciler。
Fre中的Fiber结构
React中的代码太过庞大,为了说明Fiber Reconciler的思想,我们采用Fre中的IFiber结构进行说明(Fre框架是受React启发的,两者在某些方面大致相同)
先来看一下IFiber的定义:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30export interface Attributes extends Record<string, any> {
key?: Key
children?: FreNode
ref?: Ref
}
export type HTMLElementEx = HTMLElement & { last: IFiber | null }
export interface IFiber<P extends Attributes = any> {
key?: string
type: string | FC<P>
parentNode: HTMLElementEx
node: HTMLElementEx //Fiber对应的真实DOM节点
kids?: any
parent?: IFiber<P>// 父Fiber节点
sibling?: IFiber<P>// 指向兄弟节点
child?: IFiber<P>// 子Fiber节点
done?: () => void
ref: IRef
hooks: IHook
oldProps: P
after: any
props: P
lane: number // 调度优先级相关
time: number
e: IFiber,
prev: IFiber,
d: IFiber,
laziness: any[],
dirty: boolean,
isComp: boolean,
}
Fre中的Schedule
React/Fre之所以能够采用异步中断的方式更新,靠的是Schedule的双循环机制1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52const queue: ITask[] = []
const threshold: number = 1000 / 60
const transitions = []
let deadline: number = 0
export const startTransition = (cb) => {
transitions.push(cb) && postMessage()
}
export const schedule = (callback: any): void => {
queue.push({ callback } as any)
startTransition(flush)
}
const postMessage = (() => {
const cb = () => transitions.splice(0, 1).forEach((c) => c())
if (typeof MessageChannel !== "undefined") {
const { port1, port2 } = new MessageChannel()
port1.onmessage = cb
return () => port2.postMessage(null)
}
return () => setTimeout(cb)
})()
const flush = (): void => {
deadline = getTime() + threshold
let job = peek(queue)
while (job && !shouldYield()) {
const { callback } = job as any
job.callback = null
const next = callback()
if (next) {
job.callback = next as any
} else {
queue.shift()
}
job = peek(queue)
}
job && startTransition(flush)
}
export const shouldYield = (): boolean => {
if (options.sync) return false
return (
(navigator as any)?.scheduling?.isInputPending() || getTime() >= deadline
)
}
export const getTime = () => performance.now()
const peek = (queue: ITask[]) => queue[0]
首先,Schedule会维护一个queue队列来放置任务,transitions里面只会存放flush函数,并且是外循环的入口
外循环
什么叫外循环?
- 调用schedule函数,任务被压入queue队列里
- 调用startTransition,flush被压入transitions
- postMessage执行flush
- flush的末尾又调用startTransition重新开启一轮循环
以上这个过程叫做外循环。
内循环
什么叫内循环?
注意到flush函数1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24const flush = (): void => {
deadline = getTime() + threshold
let job = peek(queue)
while (job && !shouldYield()) {
const { callback } = job as any
job.callback = null
const next = callback()
if (next) {
job.callback = next as any
} else {
queue.shift()
}
job = peek(queue)
}
job && startTransition(flush)
}
export const shouldYield = (): boolean => {
if (options.sync) return false
return (
(navigator as any)?.scheduling?.isInputPending() || getTime() >= deadline
)
}
export const getTime = () => performance.now()
deadline变量计算了什么时候应归还控制权给其他线程,这里的threshold是浏览器每帧渲染(一次完整的重绘)的最佳间隔时间
tips:浏览器每秒刷新的次数低于60hz人眼就会感知卡顿掉帧等情况,因此最多每隔1000/60=16(ms)的时间,我们就要将渲染进程的控制权交出去给浏览器渲染
内循环指的是flush函数内部while循环执行任务队列回调函数的过程。
我们再看flush函数里的while循环条件,一旦 浏览器感知到用户输入(对应isInputPending,该api在Chrome87中得到支持) 或者是内循环执行时间超过计算的deadline,就会跳出循环。如果任务队列中残留尚未执行的任务,则通过startTransition函数开启下一轮循环,继续执行。
通过内外循环交替的这种方式,我们成功实现了可中断的任务队列机制,这就是著名的时间分片机制。
关于宏任务和浏览器渲染
注意到postMessage函数,我们用它来产生一个宏任务(如果浏览器支持MessageChannel就采用postMessage的方式,如果不支持就采用原始的setTimeout)
那么为什么要产生一个宏任务呢?
我们再回到浏览器的执行过程中去,如图,这是一段关于宏任务、微任务、浏览器渲染的抽象过程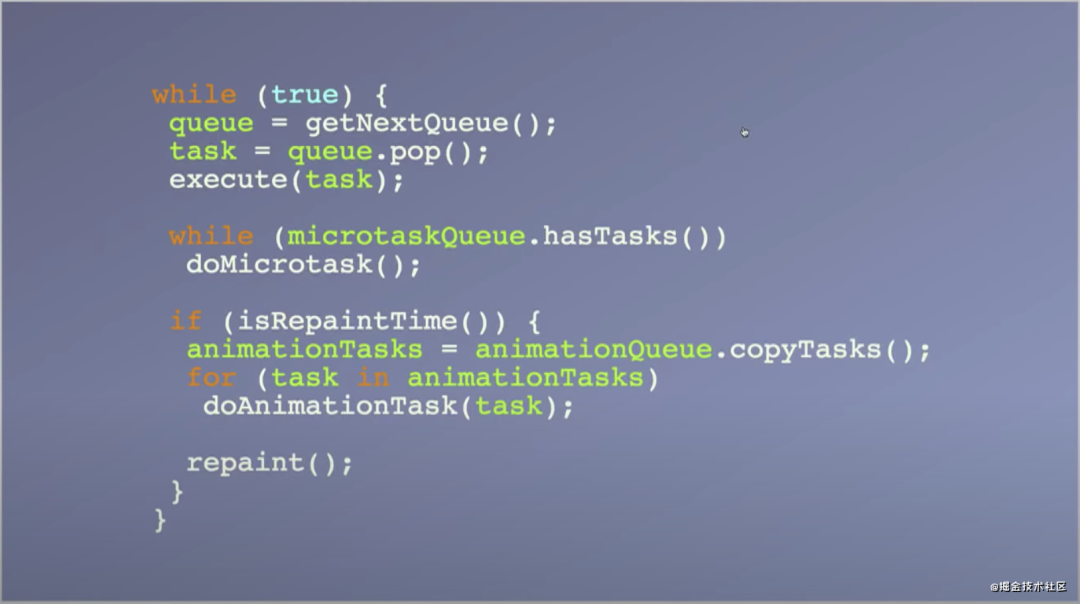
我们现在要做到:
- 将进程控制权交出去
- 能够在将来的某个时刻继续执行未完成的任务
因此宏任务能够满足我们的需求,产生一个宏任务之后,我们未完成的计算任务会在下一次循环中继续执行,进程控制权也将转交给GUI渲染线程;如果把未完成的任务放在微任务里,则需等待微任务执行结束,页面才会更新,达不到我们的要求。
写在最后的话
本文从浏览器原理、Fre源码的角度讲述了Fiber架构中的一种中断原理,而真实的浏览器渲染过程、React源码远比文中讲的要复杂,感兴趣的同学可以去研读源码。技术受限,如有错误,联系作者,我们可以一起探讨更多细节。